Городской научный семинар «Дифференциальные операторы и их приложения» 56
Городской научный семинар
«Дифференциальные операторы и их приложения»
КазНУ, каб. 213
15:00, 04 апреля 2024
Трансляция семинара в Zoom
https://us02web.zoom.us/j/6678270445?pwd=SFNmQUIvT0tRaHlDaVYrN3l5bzJVQT09
Идентификатор конференции: 667 827 0445, Код доступа: 1
Руководители семинара:
академик НАН РК М. Отелбаев, академик НАН РК Т.Ш. Кальменов,
профессор Б.Е. Кангужин, член-корр. НАН РК М.А. Садыбеков
Докладчик: КАЛЬМЕНОВ Тынысбек Шарипович
Институт математики и математического моделирования
Тема: «Интегральные представления решений коэрцитивно разрешимых задач для уравнения Лапласа»
Аннотация:
Моделирование многих стационарных физических процессов сводится к изучению краевых задач для эллиптических уравнений. Начиная с 70 годов прошлого столетия А.В. Бицадзе, А.А. Самарский исследовали новые корректные, но не обязательно краевые задачи для уравнения Лапласа имеющие важные приложения в физике плазмы. Эти задачи являются аналогом многоточечной краевой задачи для обыкновенных дифференциальных уравнений, и они получили широкое развитие для гиперболических и параболических уравнений.
Описание общих регулярных краевых задач для эллиптических уравнений даны М.В. Вишиком, а корректных, но необязательно краевых задач М.О. Отелбаевым. Основным методом этих работ является метод самосопряженных расширений симметрических операторов, построенный Дж. фон Нейманом.
В отличие от работы М.В. Вишика и М.О. Отелбаева, мы пользуемся комбинированными методами потенциала Ньютона и потенциала простого слоя. Наша первая задача - сначала описать все коэрцитивно разрешимые операторы L (коэрцитивно корректные сужения −Δ), а затем из них выделить коэрцитивно граничные операторы (коэрцитивно корректные расширения −Δ).
Следует отметить, что интегральные представления многомерных (начиная с трехмерных) классических задач Дирихле, Неймана, Робена для уравнения Лапласа получены только для шаровых секторов и для областей, ограниченных гиперплоскостями. Второй целью нашей работы является нахождение интегрального представления (построение функции Грина) классической задачи Дирихле и построение функции Грина в явном виде общих нелокальных краевых задач в произвольной области Ω.
Приглашаются все желающие!
НОВОСТИ
- Документы соискателя ученого звания ассоциированного профессора (доцента) Ергалиева Мади Габиденовича
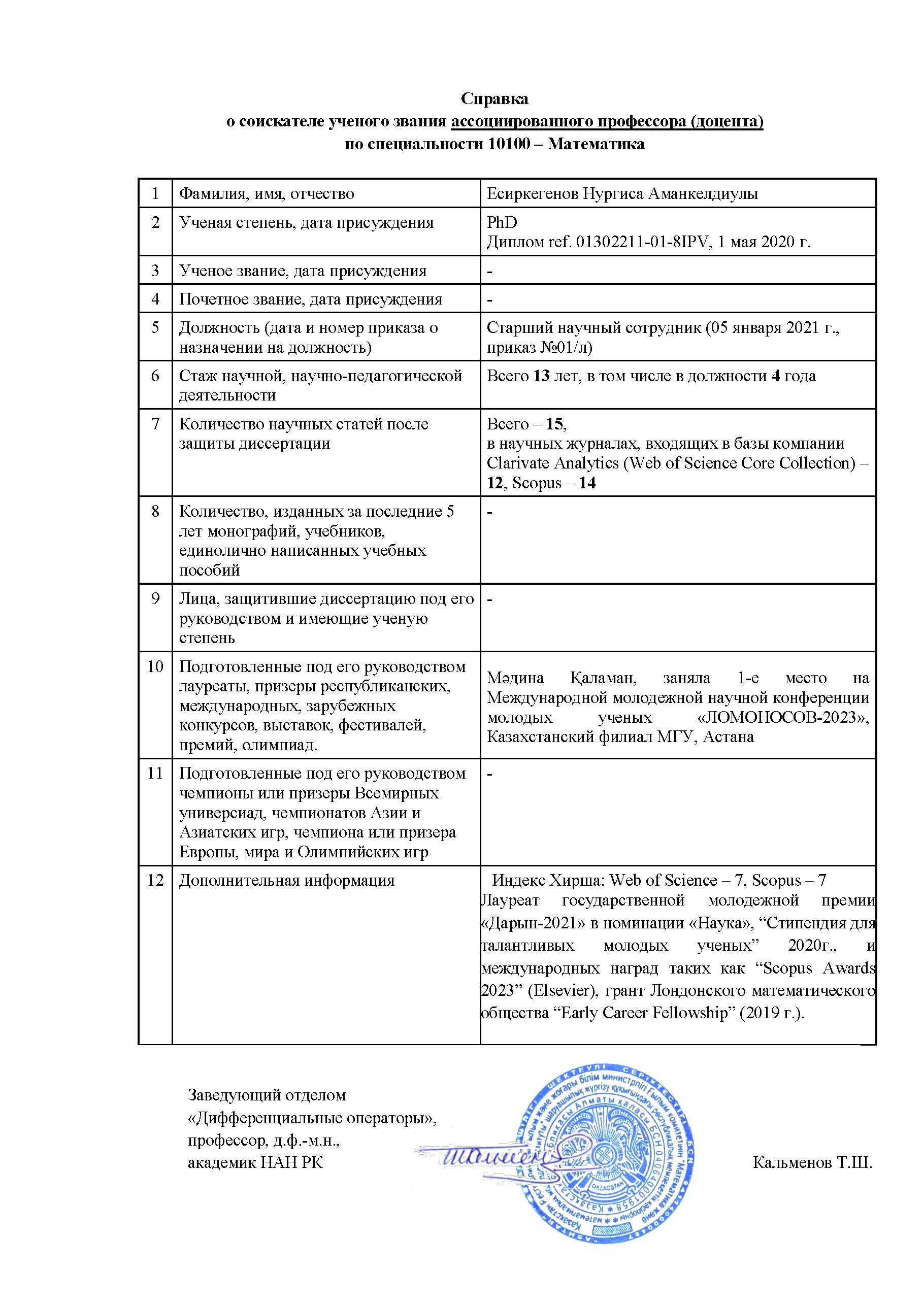
- Документы соискателя ученого звания ассоциированного профессора (доцента) Есиркегенова Нургисы Аманкелдиулы
- “Evolution Equations, Approximation and Spectral Optimization” EEASO-2024
- Документы соискателя ученого звания профессора Кадирбаевой Жазиры Муратбековны
- Документы соискателя ученого звания ассоциированного профессора (доцента) Мынбаевой Сандугаш Табылдиевной
- Информация о Законе "О научно-технической политике"
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 16-19 и 22 апреля, 2024
- Второе информационное сообщение, 16-19 апреля, 2024
- Документы соискателя ученого звания ассоциированного профессора (доцента) Сабитбек Болыс Мажитовича
- Первое информационное сообщение, 16-19 апреля, 2024
- Объявление о конкурсе на грантовое финансирование на 2024-2026 годы
- Документы соискателя ученого звания ассоциированного профессора (доцента) Касымова Айдына Адиловича
- Документы соискателя ученого звания профессора Токмагамбетова Нияза Есенжоловича
- Программа отчетной конференции по проекту "Фундаментальные исследования по математике и математическому моделированию"
- Институт математики и математического моделирования поздравляет академика С. Н. Харина с 85-летним юбилеем.
- Международный научный семинар, посвященный 50-летию Виктора Вербовского
- Документы соискателя ученого звания ассоциированного профессора (доцента) Утешовой Розы Есеновны
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 5-7 апреля, 2023
- Второе информационное сообщение, 5-7 апреля, 2023
- Первое информационное сообщение, 5-7 апреля, 2023