Городской научный семинар «Дифференциальные операторы и их приложения» 57
Городской научный семинар
«Дифференциальные операторы и их приложения»
КазНУ, каб. 213
15:00, 02 мая 2024
Трансляция семинара в Zoom
https://us02web.zoom.us/j/6678270445?pwd=SFNmQUIvT0tRaHlDaVYrN3l5bzJVQT09
Идентификатор конференции: 667 827 0445, Код доступа: 1
Руководители семинара:
академик НАН РК М. Отелбаев, академик НАН РК Т.Ш. Кальменов,
профессор Б.Е. Кангужин, член-корр. НАН РК М.А. Садыбеков
Докладчики: КАНГУЖИН Балтабек Есматович, АРТЫКБАЕВА Жанар
Казахский национальный университет имени аль-Фараби
Институт математики и математического моделирования
Тема: «Дифференциально-гранично-алгебраические уравнения и связанные с ними краевые задачи»
Аннотация: В докладе будет выделен класс гибридных задач, которые представляют смесь дифференциальных, алгебраических и нагруженных уравнений с теми или иными граничными условиями.
Подсказка от ChatGPT 3.5: Гибридные задачи, включающие различные типы уравнений и граничные условия, довольно распространены и находят применение в различных областях, таких как физика, инженерия, биология и экономика. Они часто возникают при моделировании сложных систем, где взаимодействуют различные физические или математические процессы.
Например, задачи теплопроводности могут включать дифференциальное уравнение для распределения температуры внутри материала, а также граничные условия, описывающие теплообмен с окружающей средой. Задачи теплопроводности с нагруженными членами возникают, когда в уравнение теплопроводности добавляются дополнительные источники или стоки тепла. Эти источники или стоки могут быть связаны с тепловыми источниками внутри материала, с которым мы работаем, или с воздействием внешних факторов, таких как освещение, химические реакции или электрический нагрев. Примеры приложений таких задач включают моделирование тепловых процессов в электронике, где возникают тепловые источники от электронных компонентов, или моделирование тепловых процессов в геологических структурах с учетом влияния геотермальных источников.
Или в механике сплошных сред могут возникать задачи, в которых одновременно учитываются уравнения движения (дифференциальные уравнения), граничные условия для взаимодействия с твердыми телами, а также уравнения сохранения (алгебраические уравнения).
Приглашаются все желающие!
НОВОСТИ
- Документы соискателя ученого звания ассоциированного профессора (доцента) Ергалиева Мади Габиденовича
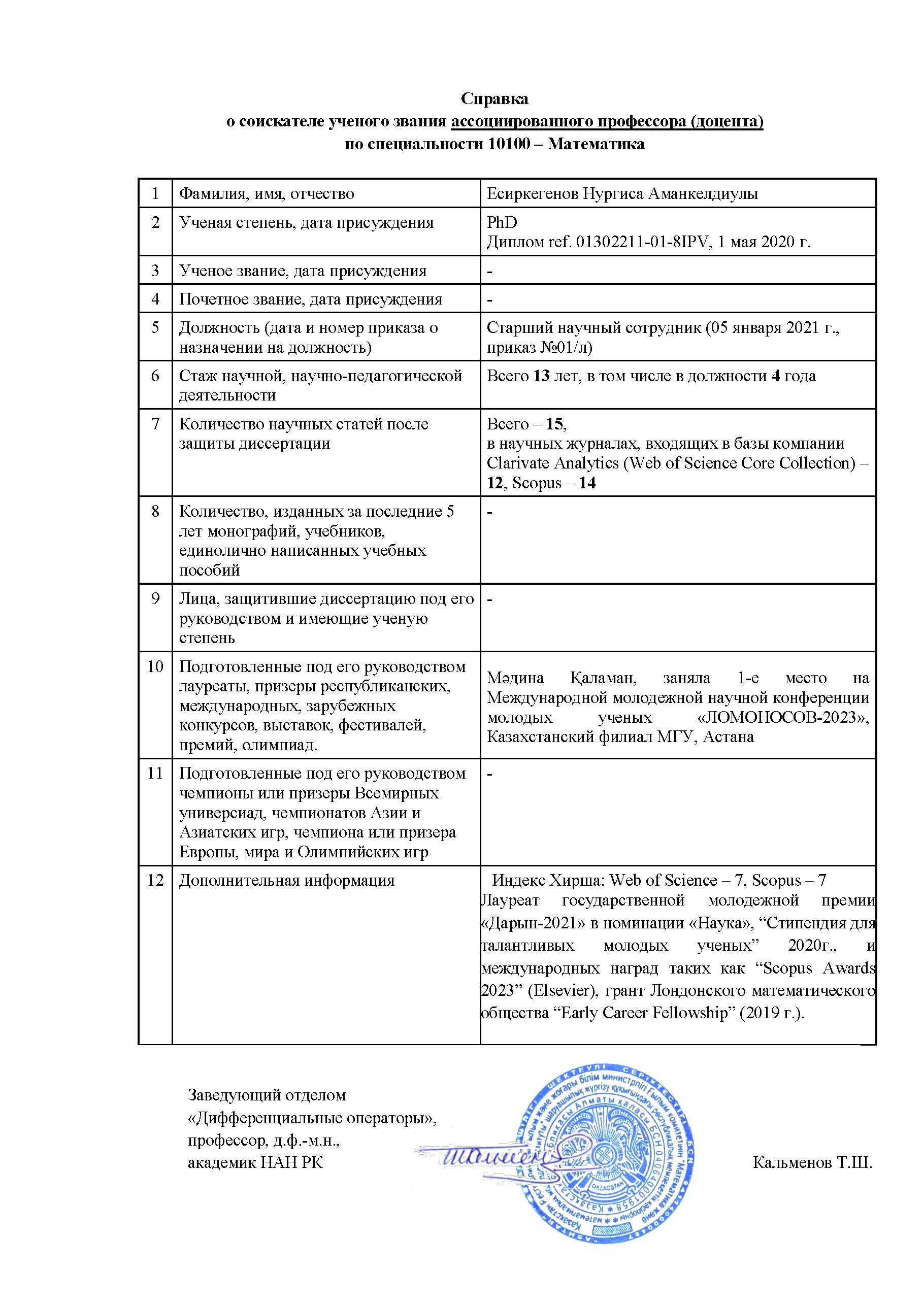
- Документы соискателя ученого звания ассоциированного профессора (доцента) Есиркегенова Нургисы Аманкелдиулы
- “Evolution Equations, Approximation and Spectral Optimization” EEASO-2024
- Документы соискателя ученого звания профессора Кадирбаевой Жазиры Муратбековны
- Документы соискателя ученого звания ассоциированного профессора (доцента) Мынбаевой Сандугаш Табылдиевной
- Информация о Законе "О научно-технической политике"
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 16-19 и 22 апреля, 2024
- Второе информационное сообщение, 16-19 апреля, 2024
- Документы соискателя ученого звания ассоциированного профессора (доцента) Сабитбек Болыс Мажитовича
- Первое информационное сообщение, 16-19 апреля, 2024
- Объявление о конкурсе на грантовое финансирование на 2024-2026 годы
- Документы соискателя ученого звания ассоциированного профессора (доцента) Касымова Айдына Адиловича
- Документы соискателя ученого звания профессора Токмагамбетова Нияза Есенжоловича
- Программа отчетной конференции по проекту "Фундаментальные исследования по математике и математическому моделированию"
- Институт математики и математического моделирования поздравляет академика С. Н. Харина с 85-летним юбилеем.
- Международный научный семинар, посвященный 50-летию Виктора Вербовского
- Документы соискателя ученого звания ассоциированного профессора (доцента) Утешовой Розы Есеновны
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 5-7 апреля, 2023
- Второе информационное сообщение, 5-7 апреля, 2023
- Первое информационное сообщение, 5-7 апреля, 2023